The Artificial Neural Network

by keshav

---

---

The Artificial Neural Network

Neurone

Neurones are a type of cell that sends and receives information or signals between the brain and the rest of the body. Nerves are formed by the connections between groups of neurones, similar to telephone cables from a telephone exchange. A picture of a typical biological neurone is shown in the figure below. It consists of a body and lots of different branches like structures called dendrites and Axons. Axons are considered as the transmitter of the signal and dendrites as the receiver of the signal. There is a gap between the dendrites and axon called a synapse.

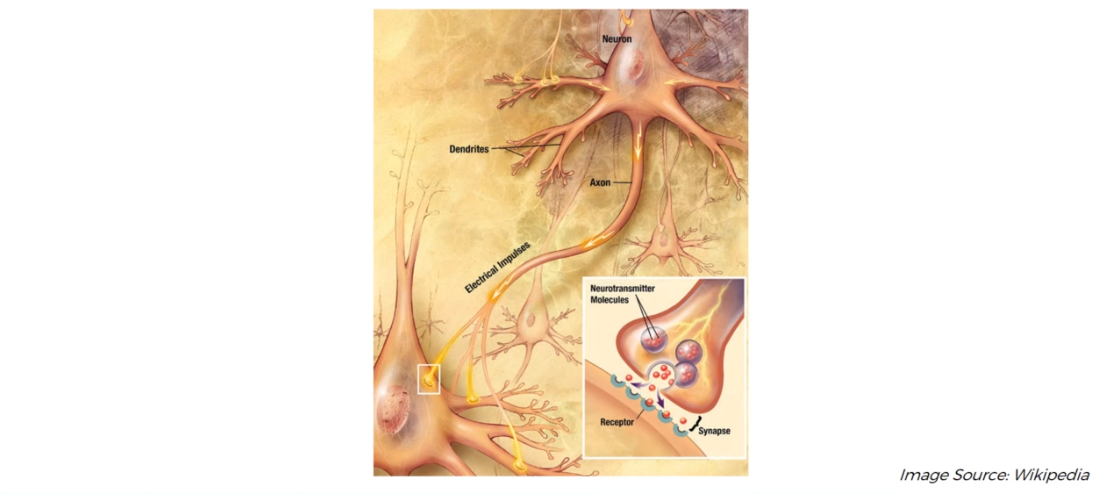
The main aim of deep learning is to mimic the same biological neurone. In this tutorial, we will see how we the structure of an artificial neurone and understand how does it learn.

 

Artificial Neurone

Following is the picture of a simple model of neurone commonly known as the perceptron. It can be divided into 3 parts: Input layer, neurone, and output layer.

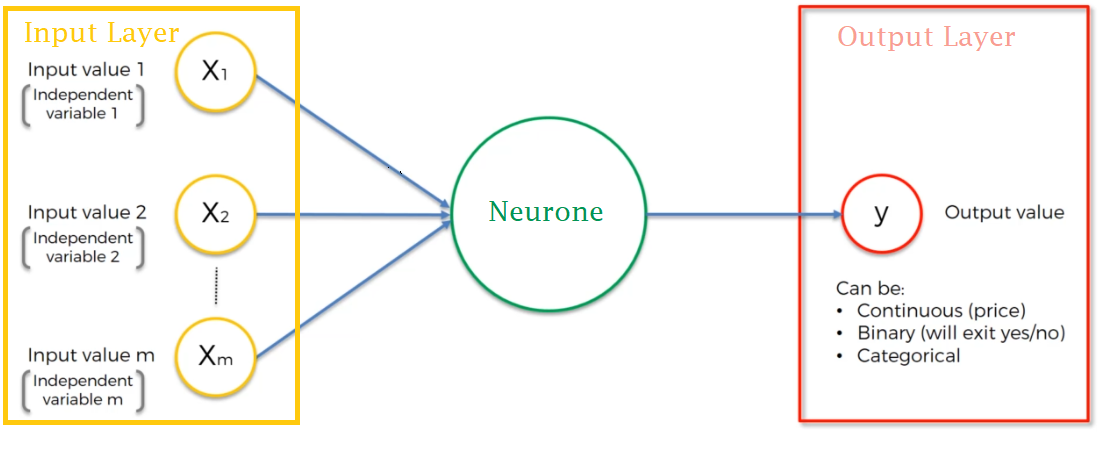
Lets understand each layers with example.

 

1. Input Layer: The input layer basically acts as a receiver of the neurone. It accepts the independent variables (X₁, X₂,…,X_m as shown in the picture above). In a real-world scenario, the inputs may be any data that describes our model. E.g. in the price of the house predicting model, inputs may be (number of rooms, location of the house, age of the house, … , etc.).

 

2. Weights: Actually this is not considered as the layer, but are the values that define how a neurone learns. The value of weights determines what signal (i.e. input variables) to pass along and how much is the contribution of the neurone. w₁, w₂,…, w_m are weights associated with X₁, X ₂,…, X_m inputs as shown in the figure above. The only thing that is performed during learning of a neural network is to adjust the value of weights such that the loss is minimized. To read how the loss is calculated read

 

3. Neurone: This is the body of our Artificial Neurone. Each and every calculation that is to be performed is done in this layer. Following things happens inside a neurone.

 

       i. Calculate the weighted sum of the input i.e.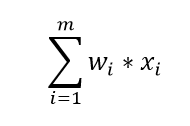       ii. Apply Activation function i.e. 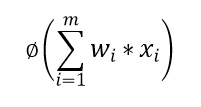      iii. The calculated value is then passed to the next layer if present.

 

In our case, we have only one neurone layer. But in real case there are several hidden layers and weights associated with those layers, thus calling it multi-layered perceptron.

 

4. Output Layer: It is the last layer of a neurone. Basically in this layer, the output given out of the neurone layer is compared with the actual output and the final prediction is made. The output may be a single output (some continuous value, e.g. price) or Binary (Yes/No, 1/0) or categorical depending upon the nature of our problem (i.e. regression or classification problem).

 

How does Neural Network learn?

The learning process of a neural network can be understood from the series of steps explained below. For this let us take a perceptron as shown in the figure below.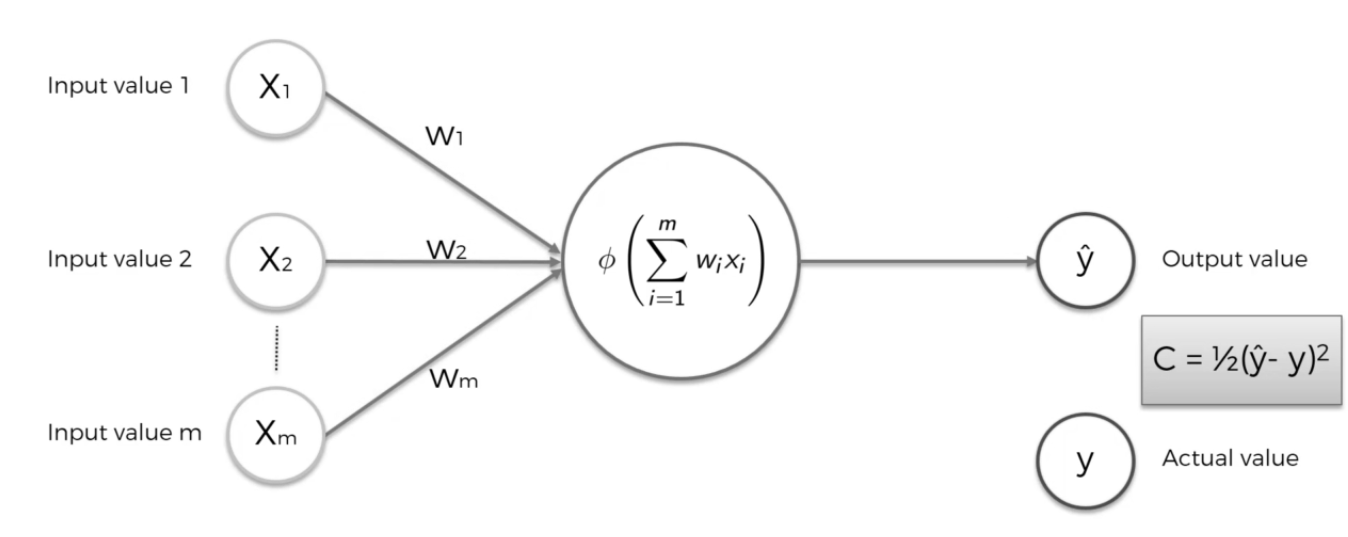

1. Let X₁, X₂,…,X_m be the inputs supplied to the perceptron and  w₁,w₂,…,w_m are weights associated with these inputs respectively.
2. First, the perceptron will calculate the weighted sum of the inputs and then will apply the activation function to it. Let yhat be the obtained output.

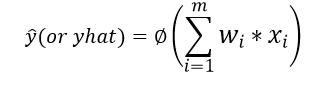
3. Let y be the actual value.
4. Now the loss/cost function is calculated from y and                   

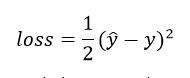Basically, the loss/cost function gives the value of how much error is there in your calculation or prediction.

[we use term loss function if we calculate error for a single training example and term cost function if we are calculating error on the overall training set. Read more]

 

5. The main aim of learning in a neural network is to minimize the loss/cost function. For the same inputs, to minimize the loss function the only way is to update the weights accordingly.
6. We use some optimization algorithm to minimize the loss function by update the weights. Gradient descent is one of the popular and commonly used optimization algorithms.
7. The updated values are fed back to the neural network in the reverse direction which is commonly called backpropagation.
8. These steps are continued until the calculated output (yhat) becomes nearly equal to the actual value (y).

 

---