Min-Max Normalization (with example and python code)

by keshav

Min-Max normalization performs on original data a linear transformation. Let (X1, X2) be a min and max attribute boundary and (Y1, Y2) be the new scale at which we are standardizing, then the standardized value Ui is given for Vi of the attribute as,

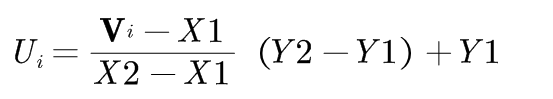
The special thing about the min-max normalization is that preserves the relationship between the original data values. If in the future the input values come to be beyond the limit of normalization, then it will encounter an error known as “out-of-bound error.”

Also Read:

Let us understand it with an example: Suppose that the minimum and maximum values for the price of the house be $125,000 and $925,000 respectively. We need to normalize that price range in between (0,1). We can use min-max normalization to transform any value between them (say, 300,000). In this case, we use the above formula to find U_i with,

V_i=300,000

X₁= 125,000

X₂= 925,000

Y₁= 0

Y₂= 1

Therefore the normalized value U_i will be 0.21875.

In python:

Here is an example to scale a toy data matrix to the [0, 1] range:

from sklearn import preprocessing
import numpy as np
X_train = np.array([[ 1., -1.,  2.],
[ 2.,  0.,  0.],
[ 0.,  1., -1.]])
min_max_scaler = preprocessing.MinMaxScaler()
X_train_minmax = min_max_scaler.fit_transform(X_train)
print(X_train_minmax)